Research

Cranmer has established himself as a leading figure on the interplay of machine learning and the physical sciences. He is the Editor in Chief of the journal Machine Learning: Science and Technology, co-authored the Particle Data Group’s chapter on machine learning, and co-founded the Machine Learning and the Physical Sciences workshop series at NeurIPS. His research interests include simulation-based inference, which leverages advances in deep learning to enable statistical inference in situations that were previously intractable. He has also explored a variety of techniques to incorporate physics knowledge and insight into machine learning architectures and training procedures. Cranmer and his group have applied these techniques to a wide range of problems including experimental high energy particle physics, theoretical high energy physics, astroparticle physics, cosmology, quantum many body physics, and lattice quantum chromodynamics.

Links to papers on INSPIRE and Google Scholar

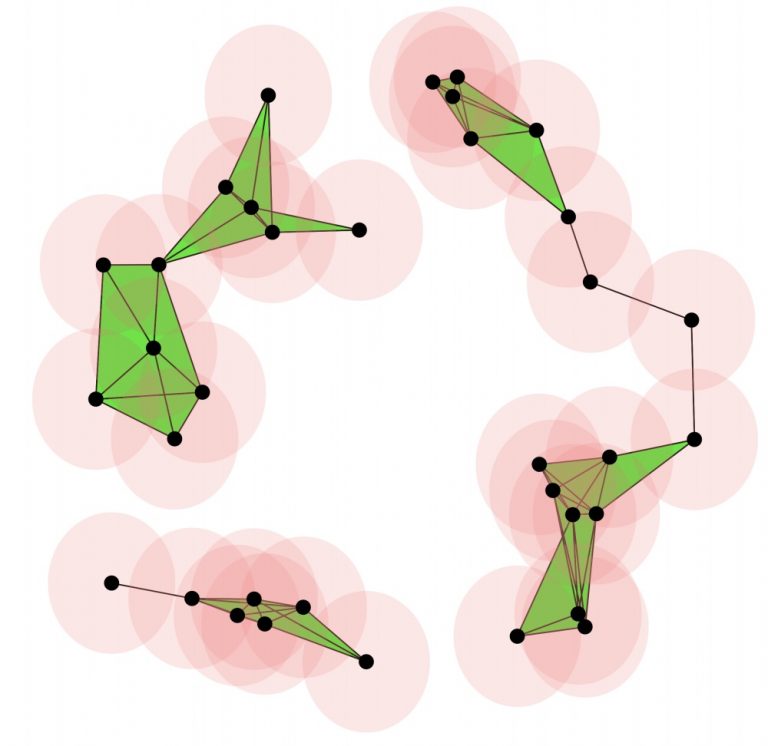
Topology provides a rigorous mathematical framework to identify interpretable patterns in noisy high dimensional data. Recent work of Gary Shiu’s group (2009. 14231), in the context of detecting and classifying phases of matter, further suggests that Topological Data Analysis (TDA) can be integrated into ML approaches to perform both unsupervised and supervised learning tasks. TDA reduces datasets into their summary statistics and yet reveals multi-scale shape information inaccessible by other techniques. The web-like features of the Large Scale Structure (LSS) of the universe make it a paragon for TDA methods. Dark matter tracers and voids have long been used by cosmologists as discerning probes of fundamental physics (e.g., neutrinos, dark energy). However, these observables can only be precisely defined and identified from noisy cosmological data using persistent topology. We have shown that TDA can provide a competitive detection of non-Gaussianity in the CMB (1712.08159) and LSS (2009.04819) data, and furthermore suggests new observables. The subsampling technique we developed to speed up TDA computation for cosmological data has wider applications, e.g., in neural science (2102.08623). The statistical tools we developed for TDA can be combined with other ML approaches to perform cosmological parameter inference of the LSS survey data.

TDA also finds applications in the high energy physics domain, e.g. in identification of classes of jets in a noisy collider environment. When combined with the low-dimensional latent representation from other ML approaches (e.g., variational autoencoder), we can obtain a combined unsupervised anomaly score or supervised event classification. As another example, we have uncovered structure and correlations in the string theory landscape using TDA (1812.06960). We further showed in 1907.10072 that stochastic optimization methods such as genetic algorithms can speed up the search for phenomenologically optimal models. This opens up the possibility to combine and contrast with reinforcement learning techniques in the study of the vast string theory landscape.

Extracting information about fundamental physics from the massive amount of complicated data of current and upcoming cosmological surveys is a very difficult task. Machine learning gives us an entirely new toolkit to solve such problems and promises to enhance or replace traditional data analysis methods.

In Moritz Münchmeyer’s cosmology group we develop machine learning methods that are specifically designed for the physical problems we want to solve, and make use of the mathematical structure of the data.

Recent papers from our group in this domain: 2105.12024, 1905.05846, 2205.12964, 2211.15161

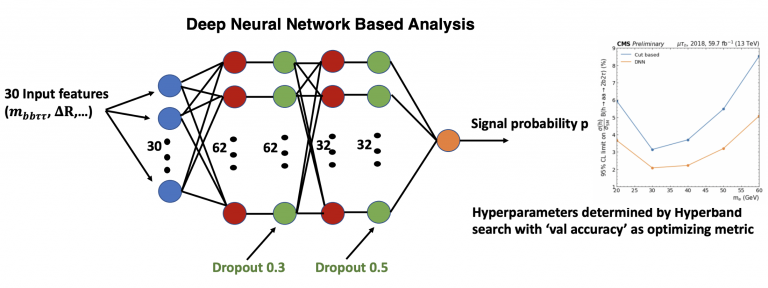
Machine learning techniques are used by the members of the CMS group led by Profs. Black, Bose, Dasu and Herndon for improving the sensitivity of new physics searches and increasing the accuracy of measurements.

Further machine learning techniques are being developed to more efficiently select events online using auto-encoders, using massively parallel processors used in the trigger systems. Because the event selection code is processed on GPUs and FPGAs ML techniques for usage on such resources is under investigation.

Pupa Gilbert uses ML in collaboration with Markus Buehler at MIT to understand patterns in nanocrystal orientations (detected with Pupa’s new synchrotron methods) and fracture mechanics (detected at the atomic scale with MD simulations by Markus Buehler).

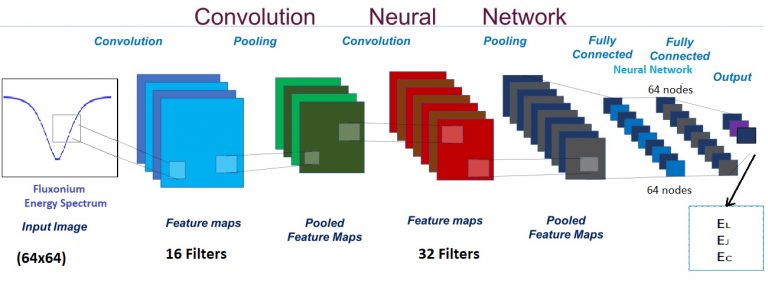
A project in Maxim Vavilov’s group aims to develop a neural network that analyzes energy spectra of a superconducting device, such as the transom or fluxonium qubit and predicts microscopic parameters of the qubit. In the case of fluxonium, we analyze the spectrum as a function of the magnetic flux through the superconductor. Our research demonstrated that even a magnetic flux dispersion curve of a single 0-1 transition provides an accurate estimate for the three energy scales of the fluxonium: charging, inductive, and Josephson energies. The inclusion of higher energy transitions makes such predictions better. Our next steps are to analyze spectra of multiple fluxoniums and make predictions for optimized single and two-quits gates for the fluxonium systems.